Gia sư ở đường Âu Cơ
Toán 9
Sau khi chúng ta học về những bài về góc nội tiếp góc tạo bởi tiếp tuyến và dây cung công dân là bài Góc cố định bên trong và góc cố định bên ngoài đường tròn thì hôm nay trung tâm gia sư Uy Tín và gia sư ở đường Âu Cơ sẽ tiếp tục giới thiệu đến các em bài tiếp theo với nội dung mang tên là bài cung chứa góc
Chương 7: Cung chứa góc
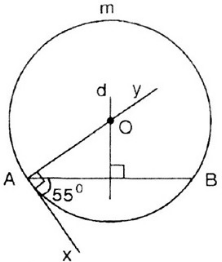
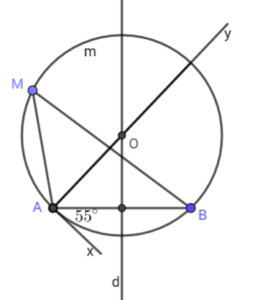
Chúng ta đi vào các kiến thức cần nhớ của bài cũng chưa gốc thì đầu tiên gia sư ở đường Âu Cơ cùng tìm hiểu về quỹ tích của cung chưa góc thì với một đoạn thẳng AB = 1 góc cho trước khi ta thấy được Nếu có như một điểm M thỏa mãn khi góc đó sẽ bằng Alpha thì ta nhìn thấy rằng hai trong đó chứa Alpha dừng trên một đoạn thẳng AB. Chú ý nghĩa quan này chúng ta cần lưu ý đó chính là hai thùng chứa gốc nói trên là hai đường tròn đối xứng với nhau qua AB điểm A đến B được gọi là quỹ tích của nó đặc biệt chúng ta cần phải lưu ý đó chính là quỹ tích của điểm M trên đoạn thẳng AB Cho trước dưới 1 góc vuông là đường tròn có đường kính AB. tiếp theo chúng ta tìm hiểu về cách vẽ khung chứa gốc thì chúng ta có một bài toán. Tìm tập hợp các điểm thỏa mãn sao cho khi không bài toán thì đầu tiên chúng ta phải đường trung trực của đoạn thẳng tiếp theo chúng ta sẽ phải thêm tia Ax và tạo ra một điểm Alpha tiếp theo chúng ta sử dụng và phải theo đường thẳng AD vuông góc với AB Gọi O là giao điểm của AI. chúng ta vẽ thêm đường tròn tâm O sao cho bán kính của nó nằm ở bờ chứa AB không chứa tia Ox vẽ được một tia tới góc Anpha. Tiếp theo chúng ta đi đến một số dạng toán thường gặp đầu tiên đó chính là dạng toán tìm cách giải bài toán theo quy cách của nó muốn chứng minh một quỹ tích của một điểm M thỏa mãn bất kì tính chất nào của một hình thì ta phải chứng minh hai phần đó chính là phần phần thì mỗi điểm có tính chất đều thuộc hình và quần đảo là một điểm thuộc hình này đều có tính chất của cái hình kia từ đó chúng ta có thể đi ra và kết luận được quỹ tích của điểm này có tính chất của điểm kia và là hình này. Thông thường thì bài toán này chúng ta tự giải theo cách tìm diện tích tăng thêm dự đoán hình này có khi chứng minh được
Tiếp theo gia sư ở đường Âu Cơ đến giải toán tiếp theo đó chính là tìm về quỹ tích là công chức của một góc alpha thì phương pháp để giải quyết bài toán này chúng ta ôn lại các kiến thức cần nhớ và tìm cách vẽ được cái đoạn thẳng cố định trong hình vẽ tương tự chúng ta tìm thêm điểm nói và tìm ra hai đoạn thẳng có định đó xác định góc alpha không đổi là như thế nào chúng ta tìm thêm các điểm quỹ tích thuộc cung chứa gấp và rừng trên các đoạn thẳng cố định đó. dạng bài toán tiếp theo chúng ta làm Đó chính là chứng minh nhiều điểm thuộc 1 đường tròn thì phương pháp để giải quyết bài toán này chúng ta cần phải chứng minh điểm đó thuộc mặt phẳng Alpha và cùng nhìn vào một đoạn thẳng cố định AB dưới 1 góc không đổi. Bài toán đề khá phức tạp trên các em cần phải chú ý và ôn lại các kiến thức Cực chỉ để có thể làm được bài toán này tiếp theo chúng ta đến rạng sáng cuối cùng là dựng cung và chứa gốc thì phương pháp để giải bài toán này chúng ta thực hiện theo những quy trình các bước sau đây đầu tiên chúng ta phải đường trung trực của đoạn thẳng đó. Chúng ta phải thêm tia X tạo thêm một đoạn thẳng AB một góc Anpha chúng ta phải tìm đường thẳng ab vuông góc với AC Gọi O là giao điểm của ah với DC Cuối cùng chúng ta vẽ đường tròn cung tròn tâm A bán kính AB và cùng tâm O sao cho cung nằm cùng với bề mặt phẳng không chứa tia X cung vừa phải đường đến chính là một vùng chứa góc Anpha nhu cầu của đề bài
Trung tâm gia sư Uy Tín và gia sư ở đường Âu Cơ vừa giới thiệu đến các em bài cũng chưa gốc bài này có những kiến thức khác mới làm và thực hiện các cách giải khác tivi cho nên cái em cần phải ôn lại kiến thức và bài thực chỉ hi vọng bài viết này có thể giúp đỡ đến các khoản chi con đường học tập và giải quyết vấn đề của mình
Mọi thắc mắc xin liên hệ về trung tâm gia sư Uy Tín và gia sư ở đường Âu Cơ để được giải đáp một cách tận tình nhất:
Địa Chỉ : 540A, Xô Viết Nghệ Tĩnh, Phường 25, Quận Bình Thạnh
Hotline : 0963.255.651
Website : giasuuytinhcm.com
Email : [email protected]