Gia sư đường CMT8
Toán 9
Sau khi kết thúc bài vừa rồi bài cung chứa góc thì hôm nay trung tâm gia sư Uy Tín và Gia sư đường CMT8 sẽ tiếp tục giới thiệu đến các em bài tiếp theo đó chính là giới thiệu về bài đường tròn ngoại tiếp đường tròn nội tiếp là như thế nào
Chương 7: Góc với đường tròn
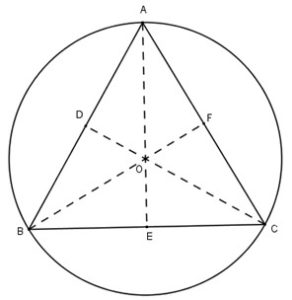
Phần đầu tiên về bài này Gia sư đường CMT8 tìm hiểu về các kiến thức cần nhớ về định nghĩa của nó thì đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp của tam giác và tự giác đó được gọi là đa giác nội tiếp đường tròn phương trình. Khi ta có một đường tròn tâm O nội tiếp tam giác abc thì đường tròn đó sẽ đi qua các đỉnh của tam giác đó như là đỉnh A điểm B và điểm C đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp lớn nhất và đa giác đó được gọi là ngoại tiếp của đường tròn chúng ta. Ví dụ như có một tam giác ABC có một đường tròn tâm O nội tiếp trong tam giác ABC có nghĩa là đường tròn này sẽ đi qua các cạnh AB AC và BC của tam giác đó. Chúng ta không có thêm một định lý đó chính là bất kì đa giác đều là có một và chỉ một đường tròn nội tiếp và chỉ có một đường tròn đó ngoại tiếp chúng ta cần phải lưu ý định lý này để chúng ta có thể giải quyết bài toán và tìm được một đường tròn phù hợp. dạng toán thường gặp ở bài này đó chính là dạng Xác định tâm bán kính và các đại lượng liên quan đến đường tròn ngoại tiếp đường tròn nội tiếp thì chúng ta thường sử dụng các kiến thức về đường tròn nội tiếp của như là đường tròn ngoại tiếp và vận dụng các kiến thức chúng ta đã học ở trên và các kiến thức chúng ta được không ở bài trước để có thể sử dụng liên kết các hệ thức và tính toán giải quyết được bài này
Tiếp theo sau khi kết thúc 3 đường tròn ngoại tiếp và đường tròn nội tiếp Gia sư đường CMT8 đến bài tứ giác nội tiếp thì ở bên này chúng ta cần nắm vững các kiến thức cần nhớ của bài đường tròn nội tiếp đó chính là tứ giác nội tiếp đường tròn và tứ giác có bốn định nằm trên một đường tròn Ví dụ như trong hình 1 chúng ta thấy được rằng tứ giác ABCD nội tiếp đường tròn tâm O và ta thấy rằng các các điểm của đường tròn nay nó sẽ đi qua điểm bên trong của tứ giác và tự giác được gọi là tứ giác nội tiếp đường tròn và đường tròn đầy là đường tròn ngoại tiếp tứ giác định lý chúng ta thấy rằng trong một đường tứ giác nội tiếp tổng các số đo góc đối diện bằng 180 độ. Nếu như một tứ giác có tổng số đo hai góc đối diện bằng 180 độ thì tứ giác đó sẽ có nội tiếp đường tròn từ định lý trên chúng ta có thể rút ra được một định lý lớp 9 bài góc A + góc C = 180 độ và góc B + góc D bằng 180 độ. Từ đó chúng ta suy ra được dấu hiệu nhận biết của tứ giác đó chính là tứ giác có tổng hai góc đối nhau bằng 180 độ và tứ giác có một góc và 1 góc đỉnh nằm ngoài đối với định đó tứ giác có 4 đỉnh cách đều một điểm Điểm đó thực tâm của đường tròn tứ giác có 2 đỉnh kè nhau cũng nhìn hai cạnh còn lại chứa một góc alpha. Các dạng toán thường gặp ở ngoài này đó chính là dạng đầu tiên chúng ta Chứng minh tứ giác nội tiếp theo phương pháp để giải quyết bài toán này chúng ta sử dụng các định lý do trên để có thể chứng minh được nó, dạng bài toán tiếp theo đó chính là chứng minh các góc bằng nhau đoạn thẳng bằng nhau và các đường thẳng song song hệ thức giữa các trận với nhau thì chúng ta sử dụng phương pháp tính chất nội tiết của tứ giác để giải quyết vấn đề này
Trung tâm gia sư Uy Tín và Gia sư đường CMT8 vừa giới thiệu đến các em bài đường tròn nội tiếp đường tròn ngoại tiếp của như là tứ giác nội tiếp các em cần phải nắm vững các kiến thức này để có thể chứng minh và làm bài tập cho thật tốt hi vọng bài viết này có thể mang lại sự hữu ích cũng như hỗ trợ cho em về các công việc học tập. Hy vong các em sẽ học thật tốt
Mọi thắc mắc xin liên hệ về trung tâm gia sư Uy Tín và gia sư đường CMT8 để được giải đáp một cách tận tình nhất:
Địa Chỉ : 540A, Xô Viết Nghệ Tĩnh, Phường 25, Quận Bình Thạnh
Hotline : 0963.255.651
Website : giasuuytinhcm.com
Email : [email protected]