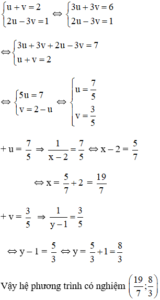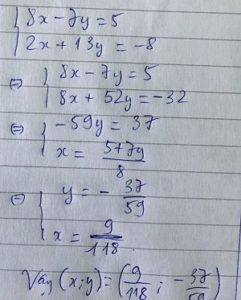Dạy kèm Củ Chi
Toán 9
Qua các bài vừa rồi chúng ta thấy được rằng chương trình Toán lớp 9 khá khó khăn và có rất nhiều kiến thức mới là vì thế chúng ta cần phải tập trung học kỳ những lý thuyết từ đó để có cơ sở vận dụng làm các bài tập sao cho thật tốt và phải rèn luyện thật nhiều. Hôm nay trung tâm gia sư Uy Tín và gia sư dạy kèm quận Củ Chi sẽ tiếp tục giới thiệu đến các em những bài tiết sau của chương hệ phương trình
Chương 3: Hệ phương trình bậc nhất hai ẩn
Sau khi kết thúc những bài đầu tiên của chương ba này chúng ta đã tìm hiểu được về những phần phương trình bậc nhất hai ẩn và hệ phương trình bậc nhất hai ẩn và cách giải phương trình bằng phương pháp Thế. Thì hôm nay trung tâm gia sư Uy Tín và gia sư dạy kèm quận Củ Chi sẽ tiếp tục giới thiệu đến các em phần giải hệ phương trình bằng phương pháp cộng đại số. chúng ta cần phải thực hiện các quy tắc cần nhớ để làm được bài giải hệ phương trình bằng phương pháp cộng đại số đó chính là gồm hai bước. Bước đầu tiên chúng ta phải công khai trừ thuế qua phương trình của hệ đã cho để được một phương trình mới dùng phương pháp mới để thay thế một phương trình của hệ phương trình và phương trình kia thì ta được thể phương trình mới hoàn toàn tương đương
Giải hệ phương trình
Một số dạng toán thường gặp ở bài giải hệ phương trình bằng phương pháp cộng đại số thì gia sư dạy kèm quận Củ Chi giới thiệu đó chính là giải hệ phương trình bằng phương pháp cộng đại số. Phương pháp để làm dạng bài này đó chính là bước 1 chúng ta nhân hai vế của một phương trình với một số nếu cần sao cho các hệ số của hai phương trình đó bằng nhau hoặc làm cho chúng đối nhau. Bước 2 thì chúng ta chỉ cần cộng và trừ 2 phương trình đầu để được phương trình thứ 3 phương trình mới tương đương kết hợp với một trong hai phương trình đề bài đã cho chúng ta giải được bài toán. Đó chính là giải hệ phương trình đưa về hệ phương trình bậc nhất hai ẩn ứng phương pháp để làm bài này đó chính là bước đầu tiên chúng ta phải biến đổi hệ phương trình đã cho về hai phương trình bậc nhất hai ẩn bước Thứ hai chúng ta sẽ giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số như đã nêu cách ở trên phương pháp một bước Thứ ba chúng ta tìm ra đáp số và kết luận
Giải hệ phương trình bằng phương phap cộng đại số
Các bài toán tiếp theo gia sư dạy kèm quận Củ Chi giới thiệu đó chính là do ăn giải hệ phương trình bằng phương pháp đặt ẩn phụ để thực hiện được phân pháp làm bài này chúng ta cần phải thực hiện 3 bước sau đầu tiên chúng ta phải đặt ẩn phụ cho các biểu thức chung có trong các phương trình và hệ phương trình đã cho để được hệ phương trình bậc nhất mới bước. Thứ hai chúng ta sẽ giải hệ phương trình bậc nhất hai ẩn bằng phương pháp cộng đại số như ở dạng bài Toán 1 đánh em bước. Thứ ba chúng ta sẽ đổi lại biến và đặc Từ đó các nghiệm của phương trình trên và giải ra tìm x và y. Dạng cuối cùng của phần bài này đó chính là dạng Tìm điều kiện của tham số để phương trình thỏa mãn điều kiện cho trước thì phương pháp bài toán này được đánh giá là rất khó và khó khăn hơn so với ba dạng toán đầu tiên nhưng chúng ta cũng sử dụng phương pháp đó chính là sử dụng các kiến thức về phương trình bậc nhất hai ẩn có nghiệm thỏa mãn các điều kiện thế hai nghiệm đó vào phương trình Mỹ sau phương trình thỏa mãn và một đường thẳng d đi qua điểm M có tọa độ cần tìm, từ đó ta có thể suy luận ra được nghiệm của phương trình
Giải hệ phương trình bằng phương pháp cộng đại số
Trung tâm gia sư Uy Tín vừa giới thiệu đến các em phương pháp thứ hai để giải hệ phương trình bậc nhất hai ẩn đó chính là phương pháp cộng đại số mong rằng bài viết này có thể chứa được nhiều kiến thức cho các em chúc em học thật tốt
Mọi thắc mắc xin liên hệ về trung tâm gia sư Uy Tín và gia sư dạy kèm quận Củ Chi để được giải đáp một cách tận tình nhất:
Địa Chỉ : 540A, Xô Viết Nghệ Tĩnh, Phường 25, Quận Bình Thạnh
Hotline : 0963.255.651
Website : giasuuytinhcm.com
Email : trinhgiasuuytin@gmail.com
