Toán 9

Ở những phần trước trung tâm gia sư Uy Tín và gia sư dạy kèm quận Tân Bình đã giới thiệu đến các em về căn bậc hai căn bậc ba cũng như các bài liên quan đến đồ thị hàm số thì hôm nay trung tâm gia sư Uy Tín sẽ giới thiệu đến các em về hệ số hai phương trình bậc nhất hai ẩn. Đây được xem là một trong những dạng toán mới là và được đánh giá là khó hơn so với phân phương trình bậc nhất một ẩn

Chương 3: hệ hai phương trình bậc nhất hai ẩn

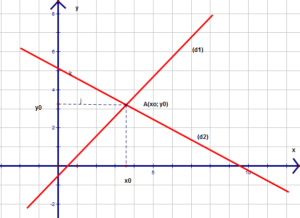
Chúng ta cùng tìm hiểu bài đầu tiên của chương này đó chính là phương trình bậc nhất hai ẩn đầu tiên chúng ta cần hiểu về khái niệm của phương trình bậc nhất hai ẩn thì phương trình bậc nhất hai ẩn lập phương trình có dạng ax + b = c trong đó thì A và B và C là những số cho trước a khác 0 hoặc b khác 0 Nếu như các số thực x 0 y 0 thỏa mãn a nhân x + b nhân y = c thì cặp số x 0 và y không có được gọi là nghiệm của phương trình đã cho. Trong mặt phẳng tọa độ Oxy mỗi nghiệm x0 y0 của phương trình y = ax + b sẽ được biểu diễn bằng bằng bột điểm có tọa độ hoàng độ x0 và tung độ y0. Giới thiệu về một số tập nghiệm của phương trình bậc nhất ai ấn Ax + By = C luôn có vô số nghiệm nếu như tập nghiệm của phương trình biểu diễn bằng một đường thẳng d. Một số trường hợp là nếu như á khác 0 và b khác 0 thì phương trình có nghiệm x sẽ bằng C phần a và c thuộc R và song song với đường thẳng d hoặc trùng với đường thẳng D nếu như a = 0 và b khác 0 thì phương trình sẽ có nghiệm x thuộc R và C bằng C phần B và đường thẳng d song song hoặc trùng với lại trục hoành. Trường hợp cuối cùng đó chính là nếu như a khác 0 và b khác 0 thì phương trình nó sẽ có nghiệm là x thuộc với R và tôi sẽ bạn chữ B phần A nguyên chất X cộng cho C phần B và đường thẳng D là đồ thị của hàm số y = – a = b nhân x cộng cho C phần b

Đồ thị phương trình bậc nhất hai ẩn

Một số dạng toán thường gặp mà gia sư dạy kèm quận Tân Bình giới thiệu đó chính là: Tìm điều kiện của tham số để một cặp số cho trước là nghiệm của phương trình bậc nhất hai ẩn. Ở dạng này thì phương pháp giải đó chính là ta sẽ có cặp số thực x không phải không thỏa mãn với ai nhưng chứa 100 B nhân y = 0 thì nó được gọi là nghiệm của phương trình đã cho. giờ tao tiếp theo đó chính là viết công thức nghiệm tổng quát của phương trình bậc nhất hai ẩn biểu diễn tập nghiệm của nó trên hệ trục tọa độ về phương pháp làm gồm hai bước đó chính là viết công thức tổng quát của phương trình Trước tiên ta phải biểu diễn X theo y Bước tiếp theo là chúng ta biểu diễn tập nghiệm của phương trình trên mặt phẳng tọa độ và đường thẳng d có phương trình ax + by = c

Cách giải hệ phương trình

Và tiếp theo gia sư dạy kèm quận Tân Bình giới thiệu đó chính là Tìm điều kiện của tham số để phương trình đường thẳng Ax + By = C thỏa mãn điều kiện cho trước thì phương pháp để giải bên này chúng ta có thể sử dụng một số lưu ý để giải bài toán đó chính là nếu như a khác 0 và b khác 0 thì phương trình đường thẳng Ax + By = C có dạng là x = – c = a khi đó d song song hoặc trùng với đội nếu a = 0 và b khác 0 thì sẽ ngược lại khi c = – c phần B Khi đó d song song hoặc trùng với lại x. cuối cùng của bài này đó chính là trắc nghiệm nguyên của phương trình bậc nhất hai ẩn thì phương pháp để giải bài toán này đó chính là tìm các nghiệm nguyên của phương trình bậc nhất hai ẩn ta làm các bước như rút gọn phương trình biểu diễn của hệ số của nó trong giá trị tuyệt đối cách tìm giá trị nguyên của biểu thức x đặt điều kiện để phân bố các biểu thức của x bằng một số nguyên T

Hệ phương trình

Bài đầu tiên trung tâm gia sư Uy Tín và gia sư dạy kèm quận Tân Bình giới thiệu đến các em đó chính là bài mở đầu của chương hệ hai phương trình bậc nhất hai ẩn. nơi này có kiến thức khá dài cho đến trung tâm gia sư Uy Tín chưa giới thiệu đến các em phần bài này mong rằng các em học thật tốt nhé

Mọi thắc mắc xin liên hệ về trung tâm gia sư Uy Tín  và gia sư dạy kèm quận 12 để được giải đáp một cách tận tình nhất: 

TRUNG TÂM GIA SƯ UY TÍN

Địa Chỉ : 540A, Xô Viết Nghệ Tĩnh, Phường 25, Quận Bình Thạnh

Hotline : 0963.255.651

Website : giasuuytinhcm.com

Email : [email protected]